leloy!
@leloykun
Followers
4K
Following
44K
Media
587
Statuses
8K
Math @ AdMU • NanoGPT speedrunner • soon RE @ ███ • prev ML @ Expedock • 2x IOI & 2x ICPC • Non-Euclidean Geom, VLMs, Info Retrieval, Structured Outputs
Joined November 2018
Sub 3-minute NanoGPT Speedrun Record. We're proud to share that we've just breached the 3 min mark!. This means that with an ephemeral pod of 8xH100s that costs $8/hour, training a GPT-2-ish level model now only costs $0.40!. ---. What's in the latest record? A 🧵.
Remember the llm.c repro of the GPT-2 (124M) training run? It took 45 min on 8xH100. Since then, @kellerjordan0 (and by now many others) have iterated on that extensively in the new modded-nanogpt repo that achieves the same result, now in only 5 min! .Love this repo 👏 600 LOC
13
48
364
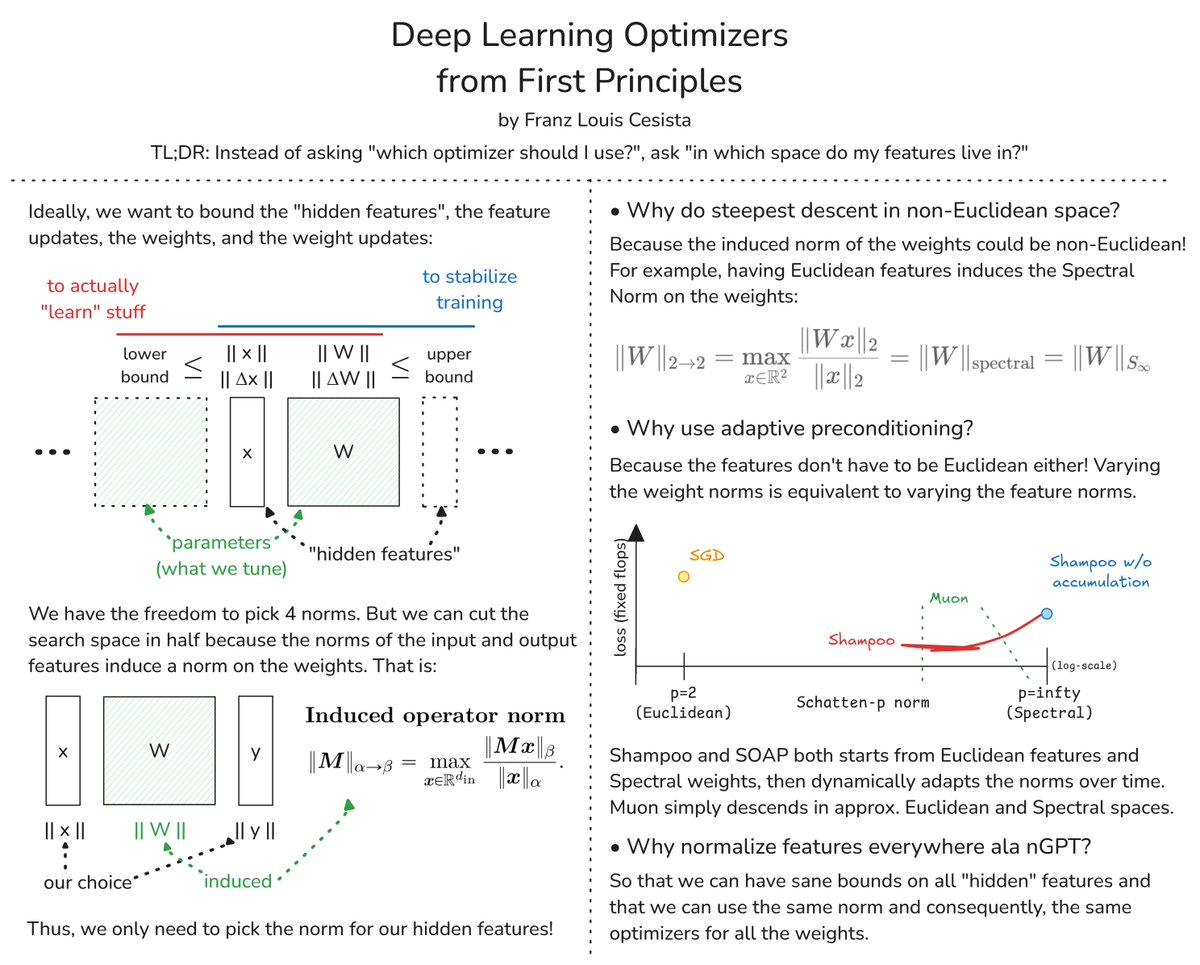
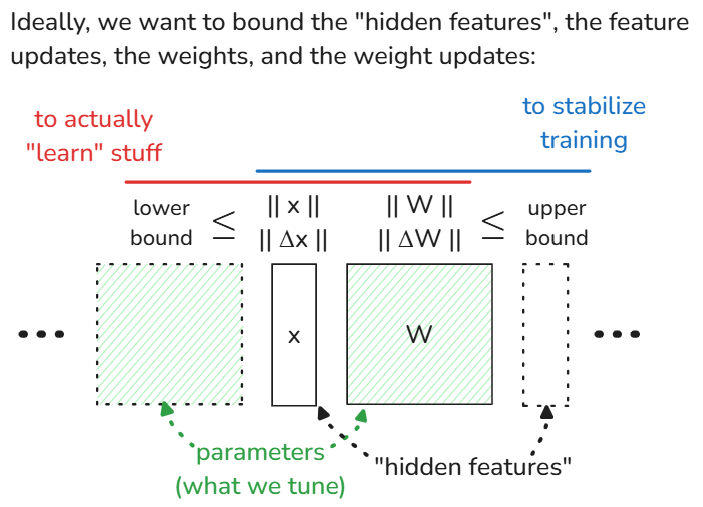
Deep Learning Optimizers from First Principles. My attempt at answering these questions:. 1. Why do steepest descent in non-Euclidean spaces?.2. Why does adaptive preconditioning work so well in practice? And,.3. Why normalize everything ala nGPT?
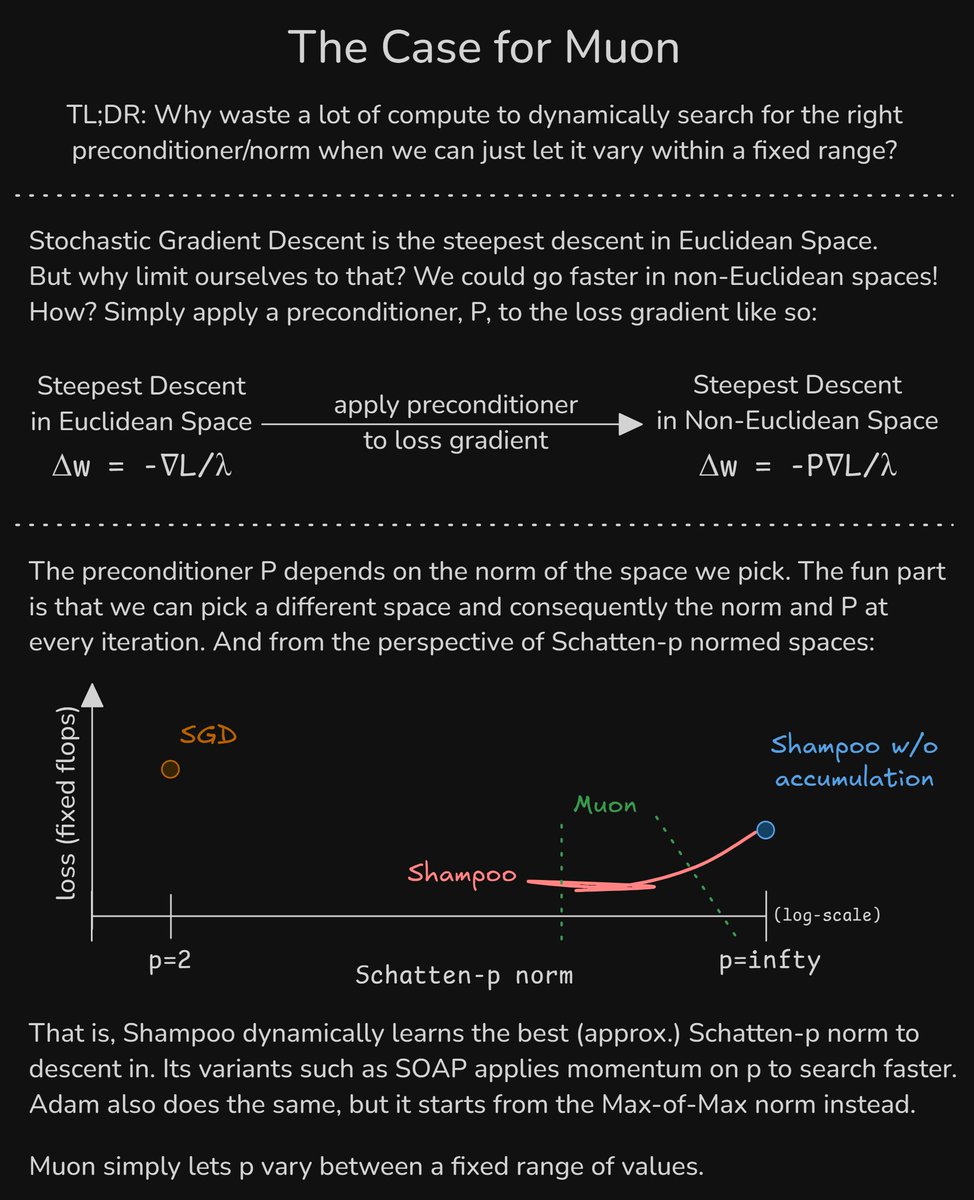
The Case for Muon. 1) We can descend 'faster' in non-Euclidean spaces.2) Adam/Shampoo/SOAP/etc. dynamically learn the preconditioner and, equivalently, the norm & space to descend in.3) Muon saves a lot of compute by simply letting the norm to vary within a fixed range
11
178
1K
Remember @karpathy's llm.c repro of the GPT-2 (124M) training run which took 45 mins on 8xH100s?. We're proud to share that we've just breached the 4 min mark!. A few years ago, it would've costed you hundreds of thousands of dollars (maybe millions!) to achieve the same result.
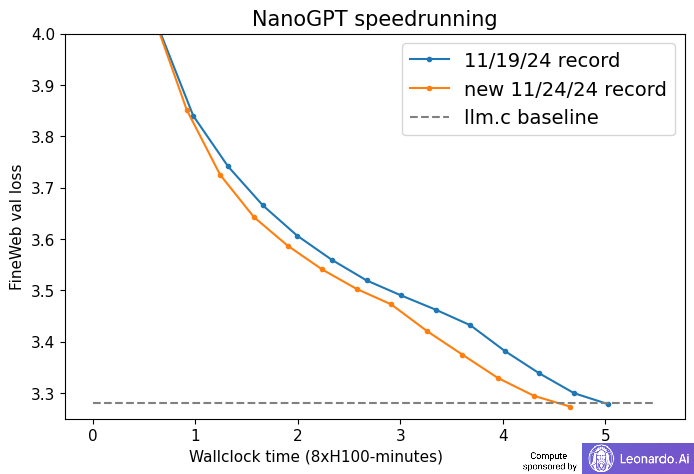
New NanoGPT training speed record: 3.28 FineWeb val loss in 3.95 minutes. Previous record: 4.41 minutes.Changelog:.- @leloykun arch optimization: ~17s.- remove "dead" code: ~1.5s.- re-implement dataloader: ~2.5s.- re-implement Muon: ~1s.- manual block_mask creation: ~5s
14
95
1K
Deep Learning Optimizers from First Principles. Now with more maths!. In this thread, I'll discuss:. 1. The difference between 1st order gradient dualizaton approaches and 2nd order optimization approaches. 2. Preconditioning--how to do it and why. 3. How to derive a couple of
Deep Learning Optimizers from First Principles. My attempt at answering these questions:. 1. Why do steepest descent in non-Euclidean spaces?.2. Why does adaptive preconditioning work so well in practice? And,.3. Why normalize everything ala nGPT?
8
101
948
Di ka iiwan ng DL certificates mo tho.
Love life first before grades;.Relationship first before acads. Hindi ka naman yayakapin ng DL certificate mo kapag umiiyak ka na. #TipsForPisayFreshies.
3
46
527
The Case for Muon. 1) We can descend 'faster' in non-Euclidean spaces.2) Adam/Shampoo/SOAP/etc. dynamically learn the preconditioner and, equivalently, the norm & space to descend in.3) Muon saves a lot of compute by simply letting the norm to vary within a fixed range
got nerdsniped by @kellerjordan0's Muon and spent time analyzing it instead of preparing for my job interview in <1 hour 😅. tl;dr.1) 3 Newton-Schulz iterations suffice for the non-square matrices.2) I propose a new Newton-Schulz iterator that converges faster and is more stable
9
31
445
we're all probably overthinking what OpenAI did with O3. here's my best guess, stitched together from tweets from OpenAI employees, their blog posts, and rumors:. 1. They collected a ton of process traces from STEM experts; they also likely mixed in synthetic data from tasks with.
14
16
343
have good news to share this week 🤗. for now, a couple of updates:. 1. We used (a JAX-implementation of) Muon to find coefficients for a 4-step Muon that behaves roughly the same as the original 5-step Muon. It's faster, but causes a slight perf drop for reasons I described in
got nerdsniped by @kellerjordan0's Muon and spent time analyzing it instead of preparing for my job interview in <1 hour 😅. tl;dr.1) 3 Newton-Schulz iterations suffice for the non-square matrices.2) I propose a new Newton-Schulz iterator that converges faster and is more stable
6
23
265
soon we'll have reasoning finetuning speedruns and y'all are gonna love and hate it
2
11
252
Adaptive Muon. @HessianFree's analysis here shows that the current implementation of Muon, along SOAP & possibly also Adam, can't even converge on a very simple loss function loss(x) = ||I - x^T * x||^2. But this issue can be (mostly) fixed with a one-line diff that allows Muon
Alright let's put Muon and SOAP head-to-head with PSGD to solve a simple loss = (1 - (x^T * x))^2, such that x is initialized as a 2x2 random matrix. At high beta both all optimizers fail but, otherwise PSGD is able to reduce the loss down exactly to zero whereas Muon can
8
14
247
got nerdsniped by @kellerjordan0's Muon and spent time analyzing it instead of preparing for my job interview in <1 hour 😅. tl;dr.1) 3 Newton-Schulz iterations suffice for the non-square matrices.2) I propose a new Newton-Schulz iterator that converges faster and is more stable
2
13
241
Here's another reason why we would want to do steepest descent under the Spectral Norm:. To have a larger spread of attention entropy and thus allowing the model to represent more certainty/uncertainty states during training!. ---. First, why do we have to bother with the
Deep Learning Optimizers from First Principles. My attempt at answering these questions:. 1. Why do steepest descent in non-Euclidean spaces?.2. Why does adaptive preconditioning work so well in practice? And,.3. Why normalize everything ala nGPT?
9
24
219
I'm gonna start posting negative results to normalize it (it wouldn't be science if we're only posting positive results). Main takeaway here is that Attention Softcapping improves training stability at the cost of extra wall-clock time (this paper even
New NanoGPT training speed record: 3.28 FineWeb val loss in 4.66 minutes. Previous record: 5.03 minutes.Changelog: .- FlexAttention blocksize warmup.- hyperparameter tweaks
8
15
215
I'm not 100% sure, but. Forcing the spectral norms of your QK weights to be low might be a bad idea cuz then your attention entropy would necessarily be a lot higher than e.g. just letting your weights grow. See more at:
5
10
207
The additive inverse of the sum of all positive integers, a thread. (1/12).
4
25
148
I hate being the "successful" cousin my titas and titos compare their kids to. "Oh, tignan mo si kuya Loy mo, blah blah blah". Thanks po. Now your kid will hate me for life.
0
12
118
The UNet Value Embeddings arch we developed for the NanoGPT speedrun works, scales, and generalizes across evals. Try it out! It's free lunch!
We are now down to 160 GPU hours for speed running SOTA evals in the 100-200M param smol model class (~31x less compute!) 🚀. Thanks to @KoszarskyB, @leloykun, @Grad62304977, @YouJiacheng et al. for their work that helped to make this possible, and to @HotAisle for their great
3
12
97
Hi y'all! Please help me get enough followers to be able to try out Twitter's new features 🙏. I'll give P300 to a random person who'd like and share this tweet (of course, you'd have to follow me so I can send you a DM). Deadline: Jan 12, 12 PM PHT.
0
63
85
Another positive reproduction of our results on the NanoGPT speedrun!. This shows that the architecture we developed (i.e. UNet Value Residuals) generalizes across datasets & evals.
Remember @karpathy's llm.c repro of the GPT-2 (124M) training run which took 45 mins on 8xH100s?. We're proud to share that we've just breached the 4 min mark!. A few years ago, it would've costed you hundreds of thousands of dollars (maybe millions!) to achieve the same result.
1
9
89
We've just opened a new track!. Latest NanoGPT-medium speedrun record: 2.92 FineWeb val loss in 29.3 8xH100-minutes.
Sub 3-minute NanoGPT Speedrun Record. We're proud to share that we've just breached the 3 min mark!. This means that with an ephemeral pod of 8xH100s that costs $8/hour, training a GPT-2-ish level model now only costs $0.40!. ---. What's in the latest record? A 🧵.
5
5
94
11/07/24 New NanoGPT speedrunning record. Changelogs:.1. Cooldown on the momentum & velocity terms in the embedding's optimizer as training winds down (c @jxbz).2. Made the value residual more flexible by splitting the lambda into two (with the sum not necessarily = 1).3.
have good news to share this week 🤗. for now, a couple of updates:. 1. We used (a JAX-implementation of) Muon to find coefficients for a 4-step Muon that behaves roughly the same as the original 5-step Muon. It's faster, but causes a slight perf drop for reasons I described in
4
1
77
Why Ateneo?. Simple: the school will treat you as a _person_ who just happens to study there.
1
1
65
Thanks for this @karpathy!. I also decided to port this to c++ cuz why not? haha.
My fun weekend hack: llama2.c 🦙🤠.Lets you train a baby Llama 2 model in PyTorch, then inference it with one 500-line file with no dependencies, in pure C. My pretrained model (on TinyStories) samples stories in fp32 at 18 tok/s on my MacBook Air M1 CPU.
4
6
58
My contributions to the latest record were actually just simple modifications to @Grad62304977's & @KoszarskyB 's prev work on propagating attention Value activations/embeddings to later layers:. 1. Added UNet-like connectivity structure on the value embeddings. This allowed us.
3
4
58
Muon currently has known issues we're still looking into. e,g.:.1. It requires a lot of matmuls. Sharding doesn't help either and even results in worse loss in most cases.2. The number of newton-schultz iterations needs to scale with grad matrix size (and possibly arch.
Imagine if conservatively going with AdamW instead of hot new stuff like Muons is the only reason this 700B/37A SoTA monster wasn't trained for the cost of **a single LLaMA3-8B**.
5
4
53
This is the overhead I'm talking abt btw:. Running the exact same code in the previous record produces roughly the same loss curve, but gets +5ms/step of overhead. While running the new code produces a better loss curve, with the same overhead. My best guess is I'm messing up my
11/07/24 New NanoGPT speedrunning record. Changelogs:.1. Cooldown on the momentum & velocity terms in the embedding's optimizer as training winds down (c @jxbz).2. Made the value residual more flexible by splitting the lambda into two (with the sum not necessarily = 1).3.
6
0
52
This girl gets prettier the more demanding her school is. Sana all ganito ka fresh!!.
0
0
48
Shopee Codeleague update:. 11th place in the ASEAN region.1st in the Philippines. Good enough, I guess. Teammates:.Raphael Montemayor.Ralph Macarasig
8
0
48
Why are malls and churches open, but not Universities?. Our priorities are fucked up.
0
4
51
I hate it when people only contact me to talk about shit like this. No, I don't want to build your app. I can come up with startup ideas on my own. Shoo
4
0
44
I was molested by gay men back in elementary. From time to time, they would wait outside the school gates and slap or rub my butt whenever I go out. I know it's not as severe as some women have experienced but it reinforced the homophobia I got from my parents. (1/4).
3
1
42
Fuck. we also qualified for ICPC 2021 (which will be held next year). AAAAAAAAAAAAAAAAAAA. I'm not ready yet!.
4
0
45
I could never date a law student. Top kasi ako pero "no one's above the law".
3
0
39
I love you all, batch 2021 💙. You deserve the best education you could get. But welp, the world's super unfair and fucked up. And we need your help to fix it. So please don't give up. Stay strong! 💪💪.
0
4
39
Not complete, but still. Congrats me!! You did well this year kaya stop feeling like you're not doing enough!
4
0
36
First is Long-Short Sliding Window Attention. This attention mechanism is inspired by the Global-Local attention in Gemma 2 (and more recent "hybrid" architectures. However, there are two key differences:. 1. Instead of mixing full attention with linear attention layers, we
2
1
38
I think I'm depressed. Well, I've always felt this way since HS pa pero I thought I'd be able to recover here in college. This is why I've been cutting classes and talking less to people lately. I'm tired and I don't wanna go to school muna. I just wanna rest :(.
6
1
34
A couple of negative results to save everyone's time:. 1. I tried a delta-like connectivity structure where the 1st & 6th layer shares the same value embedding, the 2nd & 7th, and so on, but this led to worse loss.2. I also tried letting consecutive layers share the same value.
3
0
36
I also really recommend this work by @TheGregYang and @jxbz : This one too: super information-dense works!.
2
5
36
1) I'm an atheist.2) I don't have Uniqlo shirts.3) I know how to commute.
0
1
34
@rdiazrincon I totally forgot how sets are implemented internally 😅. and this broke our metrics 💀💀.
6
0
34
Ateneans aren't really "pampered". Our classes are still challenging - just in a different way. We're just treated well. That's all.
0
3
35
Bad News: I fucked up so badly in my recent physics LT. Good News: Almost perfected my graph theory LT
1
1
30
ACET this year be like:. Can you pay for the tuition? Yes? You're in. Congrats :).
There is a lot going on and we don’t want to create more unneeded drama and stress. There will be no #ACET for SY 2021-22. Times are evolving but our commitment to academic excellence and formation has not changed. Get #readyfortomorrow, the Ateneo way.
0
2
31
> le me submits a paper to a conference. > "relevant".> "novel".> "technically sound and correct".> "Strong Reject because the references section is too long". the fuck???.
3
0
32
This'll get people killed.
How #FacialRecognition . can Reveal Your #Political Orientation . #fintech #AI #ArtificialIntelligence #MachineLearning #DeepLearning #election @analyticsinme
0
7
32
Also big thanks to @jxbz for his super insightful paper on steepest descent under different norms. @jxbz, @kellerjordan0 please let me know if I got my maths/interpretation wrong & also hoping my work helps!.
1
1
33
I've been getting misgendered more frequently lately. I know I have beautiful, lush hair, a pretty face, and a charming voice. but I'm a guy!. what the fuck!.
2
1
31
University of Tokyo's grad admissions exams don't seem so hard. what's the catch?. do I need really good recos to get in?.
7
1
32
I'm an atheist, but I think religion-bashing is cringe. There are a lot of reason why people adhere to religions - I'd even argue they're better off being in established religions like Christianity than in personality cults or brand cults.
1
1
31
(1) is why we nobody uses SGD anymore. (1) & (2) are better explained by Carlson & co's paper: Preconditioned Spectral Descent for Deep Learning in NeurIPS. For (3), I have a somewhat complete proof here: leloy! on X: "Full proof: / X.
1
1
31
Ideally, when training a neural network, we want to bound the features, the weights, and their respective updates so that:. 1. [lower] the model actually "learns" stuff; and.2. [upper] model training is stable. These bounds then depend on the norms, but which norms?
1
3
31
I don't regret picking Ateneo. Their budget for compets is super high and ProgVar's 👌👌.
2
0
29
Pisay's bureaucracy kills our innovativeness. Innovation requires spontaneity. And we can't be spontaneous if we have to record each and every little detail of what we do on some bloated ISO forms.
1
1
29
One last thing:. My JAX implementation of Muon is now in Optax!. Just install the latest development version from the Optax repo and use it as:. optimizer = optax.contrib.muon(. ).
0
0
31
Oh right, I forgot to share this here. I was in Dhaka, Bangladesh for the ICPC World Finals (it's a programming competition). Our team ended up in the dead center of the leaderboard lol
0
0
30
. I'd expect to be berated constantly and I'd be alienating my gay friends who have nothing to do with what I've experienced. That's all. Please don't judge and just spread the love!
0
1
28
Your profs train IMO participants :) You're not dumb, they just have really high standards :).
1
1
29
IQ only measures your ability to think like the person who designed the test.
0
3
28
It looks like 1 Gram iteration would suffice. I.e., estimating the spectral norm w/ `||G^T@G||_F^{1/2}`. cc @kellerjordan0
Along this direction (tighter upper bound of the spectral norm) I think we might have a free lunch leveraging the "Gram Iteration". Because we will calculate the G^2 and G^4 in the first N-S iteration, we can get a better estimation almost free. @leloykun
2
2
30
Finally, why is it a good idea to normalize everything everywhere?. Cuz it lets us have sane bounds & same norms on the features which means we can use the same optimizer for all the layers with minimal tuning!.
1
2
29
Sneak peek of the ToC of the book I'm writing. Still far from done!!
1
1
25
Insecure lang si anon guys. Maybe he/she just has nothing to be proud of aside from being in a different campus. We're all equally smart in Pisay - we took and passed the same test. Btw, may reqs pa kayo ;).
1
0
27
PSA. Tomorrow, I'll mass unfollow y'all here (even people I'm close to) and turn this into a Math and CS fan account. No hard feelings pls. I just want to detoxify my socmed life, but I also can't just delete my account since I follow a lot of scientists here rin.
0
0
26
Being able to say "money can't buy happiness" is such a privilege a lot of us can't afford to say.
0
4
27
Now, our datasets are usually Euclidean or locally Euclidean (see Manifold Hypothesis). What's the norm induced by Euclidean input and output vector spaces? The Spectral Norm!
1
0
28
We have a couple more stuff in the pipeline so I wouldn't be surprised if we somehow breach the 3 min mark by the end of the year--further reducing costs down to just $1 per run!. I haven't even brought what I've been building for a couple of months now to the game yet 😉😉. I.
2
0
27
The average developer codes just ~52 mins per day?. The fuck?. What do you all do the rest of the day?.
15
1
26
